Music Theory for Computer Applications
Eleanor Selfridge-Field
Esfield(at)stanford.edu
These pages present a brief list of definitions for discussing the principal elements of notated music.
· Scales
· Modes
· Chords
1. Scales
Scales are sets of tones used in particular works.
Multiple kinds of scales are used in most musical cultures.
What differentiates one scale from another is the particular sequence of whole and half steps it uses. Scales can start on any tone.
When scales are transposed, the defining sequence of whole and half steps must be preserved. What changes is the starting/ending position.
The number of notes in a scale may vary. The scales shown below are commonly used in Western music.
1.1. Diatonic (seven-tone) scales
Major scale (one form only)
Minor scales (three common forms)
A. Natural minor scale

B. Melodic minor scale

C. Harmonic minor scale

The steps of the scale, from lowest to highest notes, are called degrees.
Often they are called by number (1..7; sometimes given in Roman numerals, I-VII).
Other diatonic scales include two used in Balkan and Eastern Mediterranean music:
1.2. Non-diatonic scales
The pentatonic (five-note) scale
The pentatonic scale is usually given as C, D, F, G, A (effectively 1, 2, 4, 5, 6) or the equivalent.
In other five-note scales the 1.5-step gap (here D-F and A-C) can occur in other positions (e.g., F, G, A, C, D).
The pentatonic scale is particularly associated with music from Eastern Asia but it appears in many guises in the music of cultures worldwide.
The pentatonic scale is frequently found in repertories which have been transmitted orally over a long period (e.g. in African-American spirituals, Irish and Scottish folk songs).
The pentatonic scale is viewed by some as the foundation of the blues scale.
The blues scale
The blues scale is a six-tone scale with the notes C, Eb, F, Gb, Gn, Bb.
In some Asian repertories (e.g. in Japanese koto music) the 3rd and 7th tones are used but their exact pitch is determined by the performer, who controls the tuning of the instrument. In other words, the 3rd and 7th tones function as variables, while the other degrees are constant.
The whole-tone (six-tone) scale

Whole-tone scales are artificial in that, unlike most scales used in both Western and Eastern music, they do not contain the intervals called perfect fourths or fifths (which consist of closely related members of the overtone series).
The chromatic (twelve-tone) scale

Chromatic scales assume equal temperament (i.e., that D# and Eb are the same note)
They can be written many ways.
The enharmonic scale
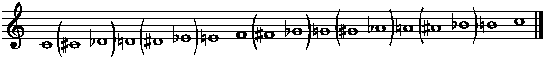
Enharmonic scales assume non-equal temperament (i.e., that D# and Eb are not the same note). Instruments used in the West before 1750 sometimes had particular tunings which were not equally tempered or split keys to accommodate multiple tunings (e.g., a D# and an Eb). The Fisk organ in the Stanford Memorial Church has ranks for both equal and mean-tone tunings.
2. Modes
2.1 Four-note modes
The ancient Greeks wrote extensively about music theory and particularly about modes. The “modes” on which they wrote were typically of four-notes (tetrachords). One tetrachord could be strung together with another. If the last note of one was also the first note of the next, the tetrachords were said to be conjunct. If they were different, the tetrachord relationship was disjunct. The first had seven notes, the second eight.
2.2 Seven-note modes
The major and minor scales that predominate in Western music originated as the Ionian and Aeolian modes. The major scale

had the special feature that its second tetrachord (G, A, B, C ascending) duplicated the whole- and half-step pattern of its first tetrachord (C, D, E, F).
Modes used in ancient, medieval, early modern, and non-Western music typically have seven tones. The vocabulary of medieval and early modern modes is quite large. Many theorists developed their own preferred list of modes.
Modes were differentiated not only by their whole- and half-step patterns but also by certain features (last tone or final, tone of greatest activity or dominant) of the pieces in which they were used.
2.3 Authentic modes
The principal modes can be thought of (for the purpose of deducing their whole- and half-step patterns) as those without altered tones beginning on one of the notes of the C-major scale (or one of the white notes of the keyboard). In the forms indicated below, the modes were known as authentic. [Sound files not included in web version]
Ionian mode

Dorian mode (final=D, dominant=A)

Phrygian mode (final=E, dominant=C)

Lydian mode (final=F, dominant=C)

Mixolydian mode (final=G, dominant=D)

Aeolian mode

2.4 Jazz and folk modes
Many other modes persist in orally transmitted repertories. The Phrygian mode is still prevalent in parts of the Mediterranean. The Dorian and Phrygian modes were still in use in the art music of eighteenth-century Europe.
Unusual modes are also used in jazz. In this context, a mode based on B (the Locrian) may occur.
Locrian mode

2.5 Plagal modes
When the final or dominant tones in church music did not correspond to the schemes of authentic modes, the mode was said to be plagal.
Hypodorian mode (final=D, dominant=F)

Hypophrygian mode (final=E, dominant=A)

Hypolydian mode (final=F, dominant=A)

Hypomixolydian mode (final=G, dominant=C)
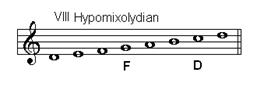
In the sixteenth century the “family” of four authentic and four plagal modes was increasingly viewed as a family of six modes of each kind. The transition from modal to tonal thinking which took place between the sixteenth and eighteenth centuries produced an enormous literature, much of which is now available in electronic form.
Online sources of music theory treatises:
1. The Thesaurus Musicarum Latinarum (Latin Music Theory, 3rd-17th centuries).
2. The Thesaurus Musicarum Italicarum (Italian Music Theory, 1529-1608).
3. Saggi musicali italiani (Italian Music Theory, 17th-18th centuries).
4. Texts on Music in English (English Writings on Music, 14th-17th centuries).
5. Traités français sur la musique (French Music Theory, c. 1600-1900).
Many of these projects include many hundreds of illustrations, and even those who do not read the languages involved may find the illustrations transparent and instructive.
3. Intervals
An interval is the distance between two notes.
If the tones sound sequentially, the interval is said to be melodic.
If the tones sound simultaneously, the interval is said to be harmonic.
The size of the interval and its name are the same in either case.
Interval sizes are named for their correspondence to an interval formed between the first note of a scale and another note, even though neither tone may be present in the present interval. Any interval that preserves the same size in half-steps and the same distance in name-class is considered to be the same as the presentation based on the primary note of the scale. For example, a perfect fourth always has a pitch-span of 5 half-steps (semitones) and a name-span of 4 letters.
3.1 Generic interval classes
The basic intervals of the major scale are these:

Note that the numeral scale starts with 1, not 0. Intervals which span a distance greater than an octave continue the series.
3.2 Specific interval classes
For reasons which can be explained both acoustically and historically, intervals are classified as belonging to one of five categories—(1) perfect, (2) augmented, (3) diminished, (4) major, and (5) minor.
Perfect, augmented, and diminished intervals
Perfect intervals employ tones which are closely related in the overtone series. They occur in all known repertories.
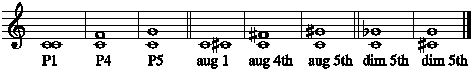
Perfect intervals which are expanded by a half-step are said to be augmented.
Perfect intervals which are reduced by a half-step are said to be diminished.
The augmented 4th and diminished 5th involving the prime are the same size in half-steps but are “spelled” differently (as a 4th and a 5th respectively).
Major intervals
Major intervals are those intervals formed by the prime and notes of the scale other than the fourth and fifth.

Major intervals are, by implication, larger than minor intervals. When a major interval is made larger by one half-step, it is said to be augmented. Augmented 3rds and 7ths are uncommon, because acoustically they are equivalent (in equal temperament) to the perfect intervals of the 4th and the 8ve.
Minor intervals
For every major interval there is a minor interval and vice-versa. Minor intervals are, by definition, one half-step smaller than major intervals.

When a minor interval is made smaller by a half-step, it is said to be diminished. Diminished 2nds and 6ths are uncommon because they are equivalent to the perfect interval of the prime and the 5th.
3.3 Intervals in minor scales and modes
The intervals formed between the first note of a scale and each successive note varies with the mode of a piece of music. This can change the frequency of occurrence of particular intervals very substantially. The intervals formed “naturally” in the natural, melodic, and harmonic minor scores is shown below:
Intervals of the natural minor scale

Intervals of the melodic minor scale

Intervals of the harmonic minor scale

3.4 Intervallic Complementarity
Every interval has a complement which, when added to it, fills an octave. The three variables of interval classification—size in half-steps, letter names, and inflection (sharp, flat, or natural)—are all required to spell the names of intervals and their complements in such a way as to show this effect.
Interval pairs formed with the tones of the major scale:

Interval pairs formed by every tone (except I) flatted:
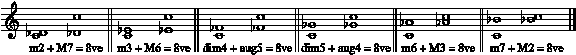
Interval pairs formed by every tone sharpened:

4. Chords
4.1 Triad (Chord) Classification
Triads (chords containing three tones) are classified by the outer interval that they fill (typically a fifth) and the intervals formed between the outer tones and the middle one.
Major and minor triads fill a perfect fifth. Augmented triads fill an augmented fifth. Diminished triads fill a diminished fifth.

4.2 Chord positions
The member notes of a triad are the root, third, and fifth. Triads are said to have a position, or configuration. A triad is in root position if the root is the lowest tone. If the third is the lowest tone, the triad is in first inversion. If the fifth is the lowest tone, the triad is in second inversion.

4.3 Basso continuo figuration
The continuous accompaniment used in almost all music of the Baroque period was provided by a basso continuo, which was often played by a keyboard instrument plus at least one string bass. The keyboard player was given only the bass line of the accompaniment and was supposed to improvise the rest by reading numerals under the notes. A bass note with no figure indicated the root position. The numeral “6” indicated a first inversion (a sixth from the lowest note to the highest). The numerals 6/4 (written vertically) indicated a second inversion (a sixth to the highest note, a fourth to the middle note).
Additional signs and numerals indicated other relationships and inflections of specific members of the triad.
4.4 Chords of the major scale
A chord can be built on each step of the major scale. In harmonic analysis the scale degree on which a chord is built is usually identified by Roman numeral. Chord built on these degrees also have names which describe their function in tonal harmony in a general way.

The names that correspond to these Roman numerals is as follows:
I tonic
II supermediant
III mediant
IV subdominant
V dominant
VI submediant
VII leading tone, triad on the leading tone
(VIII tonic)
In Latin, super means above, sub means below. The names of these functional positions is easy to remember, since everything is related to the three key-defining triads—tonic, mediant, and dominant.
The same terminology is used in any transposition of the scale, in any diatonic scale regardless of mode (major or minor), and irrespective of the positions of notes and/or inversions used in actual music.
Tonal harmony is taught in the initial stages on the basis of four-voice part-writing and there are myriad rules about voice-leading (what each voice is and is not allowed to do in relation to the others). A few fundamental rules are these:
· Voices may not move (relative to one another) in parallel fifths or octaves.
· To create four parts from a triad, it is most preferable to double the chord root, and least preferable to double the third.
These two rules give some insight into the cross-conflicts of satisfying all the rules simultaneously. If the root is always doubled, the likelihood of creating parallel fifths increases.
4.5 Chord quality in functional harmony
Systems of chord harmonization in tonal works require a determination of the key of the musical context (piece, movement, or local passage), the root, and the chord inversion. The chord quality (major, minor, augmented, diminished, etc.) may be pertinent.
The chord qualities that occur naturally in a major scale are these:

The chords in I, IV, and V are major triads.
The chords on II, III, and VI are minor triads.
The chord on VII is a diminished triad.
It often happens in actual music that the third (middle tone) of these triads is altered to change the chord quality. The major chords may become minor,
![]()
and vice versa.
![]()
Such changes are often used to facilitate modulation, that is to steer the piece to a different key from the one in which it currently is. The fundamental procedure for accomplishing this is to create an artificial dominant. Since a dominant function requires a major triad, a II converted to major enables modulation to V (d-G), a III converted to major to VI (e-A), and a VI converted to major to II (a-D).

Please note that in functional harmony the dominant must be built on a major triad irrespective of the mode of the old or new keys (i.e., even in the piece was in will be in a minor key, the dominant is categorically a major triad).
The above example introduces two further aspects of dominant-tonic progressions:
The altered triad on the dominant very frequently includes not only the members of the triad (first, third, and fifth) but also the seventh (c in the first case above, f in the second).
Except in the final cadences (ending passages) of movements and works, the triad following the dominant can be in any position. In the example above, the root of V is G, that of I C.
5. Tonal Relations
5.1 The Circle of Fifths
The Circle of Fifths was first described in the early years of the eighteenth century by Johann Heinichen, a lawyer-turned-composer. Heinichen, a harpsichordist, lived at a time when many systems of tuning were in use but when the rapid rise of string music was driving the ability to modulate freely from key to key. Wind instruments, the tuning systems of which were in most cases fixed at the time of manufacture, did not enjoy the same flexibility. They were traditionally produced in multiple sizes in order to play in different registers and keyed in a “hard-wired” way to suit them to particular keys (in mean-tone tuning). Harpsichords needed to accompany instruments of all kinds, but retuning the keyboard for every each piece in a program of music was tedious. Equal temperament was an increasingly accepted one-size-fits-all solution to the problems of retuning. It lacked the mathematical elegance of some rival systems, but its simplicity made it a standard that continues to this day. Heinichen’s diagram (1728) appears below:
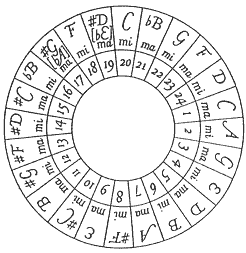
In Heinichen’s visualization the Circle is somewhat hard to decode immediately because the major-key (odd numbers, ma) and minor-key (even numbers, mi) cycles are interleaved. [Modern representations tend to place the corresponding minor tonalities in an inner circle.] Heinichen did not anticipate today’s convention of representing minor keys by lower-case letters, but the letters associated with even numbers should be read that way. A (a) is the relative minor of C Major (it is the key that shares the same key signature).
The Circle of Fifths is a two-dimensional schematic view of relationships between the chords rooted on each of the twelve tones of a chromatic scale. These chord-roots are arranged by intervals of a fifth (clockwise direction) or fourths (counter-clockwise direction). Because the circle is closed, the wheel conveys the idea that eventually, through a series of twelve modulations, one can traverse tonalities based on each of these twelve tones.
Modulation (the temporary establishment of a new tonal base) is a fundamental principle of musical structure in tonal repertory. Many of the forms that distinguish one musical genre from another depend on functional harmonic schemas, in which key changes are often coincident with thematic change. Many such schemes are specific to mode: that is, they work one way in a major key and a slightly different way in a minor key.
In the binary (two-sectional) form called a minuet, for example, the first half of an example in major would modulate from I (tonic) to V (dominant), while the second would shift back from V (dominant) to I (tonic). Since most movements in binary form the minuet also employs a particular convention relating to repetition of its two halves.
This can be represented schematically as I-V-V-I in terms of its overall harmonic structure, but because of repetitions, the realized form is I-V-I-V-V-I-V-I.
In specific instances this could mean presenting material based on chords rooted on C-G-C-G-G-C-G-C, or Eb-Bb-Eb-Bb-Bb-Eb-Bb-Eb, or ten other sequences containing a proximal fifth relationship.
In a formal minuet of the classical repertory, this binary structure and its repetitions encapsulate a second binary structure called a trio. It contains contrasting thematic material and may begin in a contrasting key but has a structure identical to that of the outer minuet. After the trio is performed with its repeats, the minuet is repeated without repeats. The overall form is said to be ternary (three-sectional; i.e., minuet-trio-minuet).
A minuet (or other structure defined by harmonic/thematic coincidence) in a minor key often modulates to the associated major key.
Minor Keys
Minor keys, having a richer legacy of origins than major keys, are more various in their behavior and thus is their treatments in relationship to harmony and form. In the context of tonal harmony, any given minor key has both a relative major and a parallel major.
The relative major shares its key signature with the minor scale.
The parallel major shares its key name with the minor scale.
The image below shows the Circle of Fifths in terms of key signatures only.

The Roman numerals of functional harmony are written in lower case (i.e., i-v) when they signify chords considered (by virtue of their intervallic size and structure) to be minor. Upper-case numerals signify major chords. [In textual references, A Minor and A Major are normally written thus.]
The image below shows the relationship of the chords built on degrees of the major scale in relation to the Circle of Fifths:

Chordal progressions
Not all the chords built on major-key roots are major, nor are all the chords built on minor-key roots minor. The chords which occur naturally (that is without the introduction of any tones outside the scale) on any given scale, major or minor, are unvarying in the major, but variable in the minor mode because of the multiple forms of the mode itself. [See Chord Quality in Functional Harmony.]
5.2 Geometries of Tonal Harmony
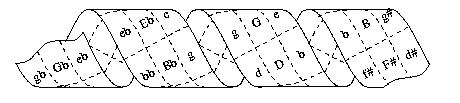
Recent theories of tonal harmony (Purwins, Chew, Sapp, Lerdahl, et al.) postulate that the set of relationships mapped onto fifths progressions does not form the two-dimensional circle of Heinichen but rather a three-dimensional spiral, helix, or toroidal structures. The third dimension of tonal relations comes from the progression through pitch-space ever upward or downward, with no touching of end-points. For practical reasons pitches beyond the range of human hearing are ignored.
In the representations below, the first shows the sequences of keys from double flats through double sharps in a snail-shell formation.
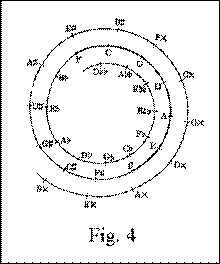
Hendrik Purwins’ toroidal views of pitch relationships (ToMIR) are shown in multiple ways below. In the next view, the “circle” of fifths is in the middle line, while the corresponding relative minor keys are placed in the top row and the corresponding parallel minor keys are in the bottom row:
The “circularity” per se is indicated in the wrapped view below:
For full color views of Purwins’ three-dimensional models and their explanations, see http://www.ni.cs.tu-berlin.de/~hendrik/research/ToMIR.html.
In on-going research Craig Stuart Sapp has created chord-quality maps (“keyscapes”) of both tonal and atonal works. Key regions which are adjacent in the Circle of Fifths are mapped onto colors which are adjacent in the rainbow or on a color wheel. When one moves up from the baseline in a keyscape one is seeing progressively bigger windows of time. See http://www-ccrma.stanford.edu/~craig/keyscape/.
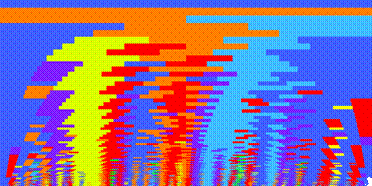
In the Bach D-Major Prelude (Well-Tempered Clavier, I; above) and the corresponding fugue (below) similar progressions are observable, although the differences of detail (reflecting the different textures of the works) are also obvious.
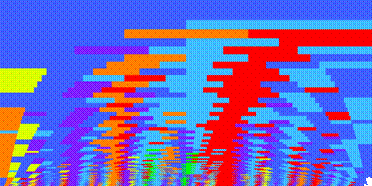
Sapp has several other geometrical representations of harmonic content, among them domes and triangles.
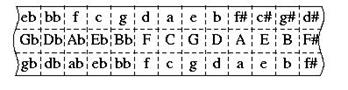
5.3 Enharmonic Notation, MIDI, and the Base-40 Pitch Representation
In equal temperament, every physical position on a musical instrument can have several names. On a piano keyboard, the black note between C and D can be indicated as a C# (C-sharp) or a Db (D flat). In more complex music, the physical C can be a symbolic B# (B-sharp) or a symbolic Dbb (D-double flat). In other words, every half-step increment changes the name of a pitch. Before equal temperament pitch pairs such as C#/Db did not have a common frequency equivalent. It is equal temperament that linked a common frequency to these names.
The encoding of music in the1960s and 1970s sometimes used only pitch-letter codes, with no indication of inflection (sharp, flat, natural) or octave. Thus there were seven codes per octave. This was severely limiting.
The fact that MIDI data-streams encode a physical key number keeps like-named pitches on separate octaves distinguished but it under-specifies pitch-inflection. This is severely limiting in notational and analytical applications in tonal repertories.

Enharmonic notation (the variability of spelling in relation to a fixed frequency, e.g. C#/Dd) complicates the achievement of correct visual and symbolic grammar in the generation of musical notation from reduced pitch-maps, such as the 12-tone/octave nomenclature of MIDI key numbers. Several approaches to the reduction of errors in the interpretation of MIDI key numbers have been proposed.
Among them, the one used here (CCARH) for contextual accuracy of enharmonic notation in printing, transposition, and theory-based analysis at CCARH is Hewlett’s base-40 system (http://www.ccarh.org/publications/reprints/base40/), in which pitch-name, pitch-inflection, and octave number are synthesized on a single (integer) number-line. The pitch-articulation possible is compared with simpler systems below:

The base-40 system has also been used to preserve symbolically encoded enharmonic spellings in MIDI data by mapping inflection information (excluded in MIDI key-number bytes) in unused bits of the MIDI velocity byte. This enriched MIDI format is called MIDIPlus. (See http://www.ccarh.org/ ~esf/esf_courses/Base40_abstract03.pdf.)
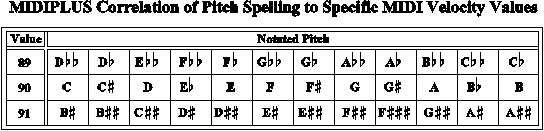
The tweaked bits can be distilled mentally by noting the differences of notation and numerical representation in the two examples below.


For the complete deck of slides see from my presentation “Base-40 Arithmetic: Implications for Notation-Based Applications” (http:/www.ccarh.org/~esf/3B-Base-40 Arithmetic/.
Eleanor Selfridge-Field
Last updated: 29 January 2004